Homepage von Peter Rachow Startseite - Home

Zur Mathematik des Bühlmann-Dekompressionsalgorithmus

Bei den von Prof. A.A. Bühlmann seit den 60er Jahren an der ETH Zürich entwickelten Dekompressionsalgorithmen mit der Bezeichnung ZH.. (für 'Zürich', z. B. ZH-L16 bzw. das Verfahren ZH-L12) handelt es sich um sog. "Haldane"-basierte Dekompressionsalgorithmen, bei denen der menschliche Körper modellhaft in eine bestimmte Anzahl repräsentativer Modellgewebe (sog. Kompartimente ) unterteilt wird, mit deren Hilfe dann die eigentlichen Dekompressionsberechnungen durchgeführt werden. Daher bezeichnet man Rechenverfahren dieser Art auch als "Gewebemodelle" bzw. "Kompartimentmodelle". Diese Verfahren haben eine weite Verbreitung gefunden und werden heute in vielen Tauchcomputern und Dekompressionsprogrammen bzw. als Grundlage für die Berechnung von Austauchtabellen (Dekompressionstabellen) angewandt.

Die kompartimentorientierten Rechenverfahren basieren i. W. auf zwei Grundannahmen. Man geht davon aus, dass jedes Gewebe des Körpers

a) sich unter Überdruck mit einem Inertgas aufsättigt und dabei eine bestimmte Halbsättigungszeit für dieses jeweilige Inertgas besitzt, sowie
b) einen bestimmten Inertgasüberdruck in Relation zum (niedrigeren) Umgebungsdruck symptomlos tolerieren kann.

Erst wenn der Inertgasüberdruck eines Gewebes in Relation zu dem gerade herrschenden Umgebungsdruck (der durch die Tauchtiefe gesetzt wird) zu groß ist, die Gasspannung innerhalb des Gewebes also einen bestimmten Wert im Verhältnis zum Umgebungsdruck überschreitet, treten Gasblasen hinreichender Größe im Körper bzw. dem betroffenen Gewebe auf und es kommt in der Folge zu Symptomen der Dekompressionskrankheit (DCS).

Ziel einer regelgerechten Dekompression ist es demzufolge, während der druckentlastenden Phase eines Tauchganges den umgebenden Druck (p.amb) zu jeder Zeit so groß zu halten, dass sich alle Gewebe zu jeder Zeit unterhalb dieser kritischen Schwelle befinden, dadurch regelgerecht entsättigen können und keine Gasblasen signifikanter Zahl und Größe erzeugt werden..

1. Der Dekompressionsalgorithmus ZH-L16

ZH-L16 ist der am weitesten ausentwickelte Dekompressionsalgorithmus aus dem Spektrum der Bühlmannschen Arbeiten. Er ist bestechend einfach und benutzt lediglich 3 simple mathematische Gleichungen um die Dekompressionsgegebenheiten zu ermitteln. Verschweigen darf man allerdings nicht, dass er vom Standpunkt der Mathematik her betrachtet einige (für die Praxis allerdings vernachlässigbare) Schwächen und Unsauberkeiten aufweist, was u. a. auch an der später zu diskutierenden Berechnung der Nullzeiten deutlich wird.

Zur Struktur des Algorithmus:

Die erste der verwendeten drei Formeln ermittelt, unter welchem Partialdruck das Inertgas aufgenommen wird (inspiratorischer Inertgaspartialdruck, p.i.i.g, p ressure of i nspirated i nert g as). Diese Gleichung ist also die Inspirationsgleichung .

Die zweite errechnet davon ausgehend den jeweiligen Inertgaspartialdruck (Physiker sprechen auch von "Gasspannung", vergleichbar mit der Aufladespannung eines Kondensators) eines Gewebes ( p.i.g, p ressure of i nert g as, siehe Gl. II). Sie wird auch als Sättigungsgleichung bezeichnet, denn sie bildet den jeweiligen Sättigungszustand eines Gewebes zu jeder Phase des Tauchgangs ab.

Die dritte Gleichung gibt an, welchen äußeren Druck ( p.amb, a mbient p ressure) ein Gewebe gerade nicht unterschreiten darf, damit keine Gasblasen aus dem Gewebe austreten (siehe Gl. III). Diese Formel berechnet also die gerade noch symptomlos tolerierte Gasspannung des Gewebes im Vergleich zum Umgebungsdruck. Man könnte sie daher auch Toleranzgleichung nennen.

Zusammenfassend ausgedrückt: In die Funktion der Sättigung eines Gewebes mit Inertgas eingehende Größen sind

a) die Tauchzeit (Expositionszeit),
b) die Tauchtiefe (also der daraus abgeleitete Umgebungsdruck p.amb)
c) der Inertgasanteil im Atemgasgemisch und
d) der Umgebungsluftdruck über Wasser, der mit b) zusammen den Gesamtdruck in der Teife ergibt.

Der Umgebungsluftdruck ist nicht vernachlässigbar, weil er auf die Wasserfläche wirkt und daher zum Wasserdruck addiert werden muß. Bedeutung erlangt er daher insbesondere bei der Dekompression, weil nach dem Beenden der Dekompressionsphase weiterhin Inertgas von den Körpergeweben abgegeben wird, die Entsättigung also fortschreitet. Wenn der Umgebungsdruck geringer ist als z. B. der Luftdruck auf Meereshöhe, muss im Wasser länger dekomprimiert werden um die im Gewebe herrschende Gasspannung weiter abzubauen. Dieses Faktum erhält Bedeutung beim Fliegen (herabgesetzter Kabinendruck, ca. 600 mBar) und beim Bergseetauchen.

2. Die Mathematik der Bühlmann-Gleichungen

Sehen wir uns die einzelnen Gleichungen genauer an:

2.1 Berechnung des inspiratorischen Inertgaspartialdruckes

Bei der Gasaufnahme in den Körper steht der Partialdruck des Inertgases (meistens Stickstoff, u. U. Helium bzw. ein Gemisch von beiden) in einem bestimmten Verhältnis zum Umgebungsdruck (Wasserdruck), er ist von diesem funktional abhängig. M. a. W.: Je tiefer getaucht wird und je höher der Inertgasanteil im Atemgas ist, desto höher ist der einatemseitige Inertgaspartialdruck.

Dieser vermindert sich noch geringfügig um den Dampfdruck des in der Atemluft gelösten H ₂O, der mit 0,063 bar (=Sättigungsdampfdruck von H ₂O bei der Körpertemperatur von 37°C) angesetzt wird.

Es gilt:

(I)

p _iig : Einatemdruck (Inspirationsdruck) des Inertgases
p _sH2O : Sättigungsdampfdruck von Wasser bei T=37°C
p _amb : Umgebungsdruck
f _ig : Anteil des Inertgases im Atemgasgemisch (bei N ₂: ~78%)

2.3 Berechnung des Inertgaspartialdruckes im Gewebe

Nach einer bestimmten Einwirkungszeit (Tauchzeit) des unter erhöhtem Umgebungsdruck eingeatmeten Inertgases ist dessen Partialdruck in den verschiedenen Körpergeweben funktional angestiegen. Die Funktion hat dabei exponentiellen Charakter, d. h. die Aufsättigung eines Gewebes ist endlich. Sie strebt bei einer konstanten maximalen Tauchtiefe einem Endwert zu, nämlich dem Inertgaspartialdruck im Gewebe vermindert um den Dampfdruck des im Atemgas gelösten H ₂O (s. o.).

Wichtiges Moment hierbei ist die Halbsättigungszeit eines Gewebes, also die Zeit, nach deren Verstreichen das Gewebe noch die Hälfte des in der vorigen Zeitspanne erhaltenen Inertgaspartialdruckes aufnehmen kann.

Dieser Partialdruck eines Inertgases im Gewebe nach einer bestimmten Zeit t errechnet demnach sich zu:

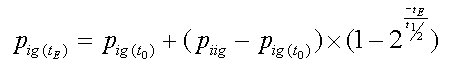
(II)

p _{ig (tE)} : Inertgaspartialdruck im Gewebe nach Expositionszeit t _E .
p _ig(t0) : Inertgaspartialdruck im Gewebe zu Beginn der Expositionszeit t _E .
p _iig : Einatemdruck (Inspirationsdruck) des Inertgases (siehe Gl. I)
t _E : Einwirkzeit (Expositionszeit), beliebige Zeitspanne, in min..
t _1/2 : Halbwertszeit des Gewebes in min.

Zentrales Element dieser Gleichung ist der Sättigungsfaktor p _iig - p _ig(t0). Ist der Inertgaspartialdruck im Atemgas ( p _iig ) höher als der des Gewebes p _ig(t0) ist der Faktor positiv, es erfolgt Aufsättigung. Beim Auftauchen (Dekompression) kehrt der Sättigungsfaktor p _iig - p _ig(t0) dann sein Vorzeichen um, die abgegebene Inertgasmenge ist größer als die neu aufsättigende, die Gasspannung der Gewebe verringert sich. Ob aufgesättigt oder entsättigt wird, hängt also von der Relation von inspiratorischen zu bereits im Gewebe vorhandenem Inertgaspartialdruck ab.

Mit dieser Berechnung erhält man für jede Tauchgangsphase einen Wert für den Inertgaspartialdruck in einem bestimmten Gewebe.

Anmerkung: Bei genauer Betrachtung wird man erkennen, dass Gl. I in Gl. II enthalten ist, sowie Gl. II in Gl. III eingeht. Strengenommen könnte man also eine einzige Gleichung daraus aufstellen, was aber nicht mehr übersichtlich und nachvollziehbar wäre zumal Gl. II und Gl. getrennt gerechnet werden, um´z. B. bei einer Dekompressionssoftware den aktuellen Zustand der Gewebesättigung separat abspeichern zu können.

2.3.1 Anwenden der Formeln während der Kompressions- und Isopressionsphase

Um die Betrachtungen zu vereinfachen, teilt man einen Tauchgang in 3 Phasen auf: Abtauch- (Kompression), Grund- (Isopression) und Auftauchphase (Dekompression). Während des Abtauchens (Kompression, i. e. steigender Druck) und des Aufenthaltes auf einer bestimmten Tiefe (Isopression, iso = "gleich", i. e. gleichbleibender Druck) sättigen sich die Gewebe mit Inertgas (i. W. Stickstoff bzw. Helium) entsprechend des inpisratorischen Inertgaspartialdruckes und ihrer Halbsättigungszeiten auf.

Um die jeweilige Aufsättigung des/der Inertgase(s) in den verschiedenen Geweben zu berechnen, müssen die Halbwertszeiten der einzelnen Teilgewebe des Körpers (Kompartimente) bekannt sein. Bühlmann hat dazu, wie beschrieben, den menschlichen Körper im Modell ZH-L16 in 16 Teilgewebe unterteilt und nennt dazu für jedes Inertgas 16 korrespondierende Halbwertszeiten, die im Bereich von 2,65 min. bis 635 min. (für N ₂) liegen. Für Helium (He) liegen sie zwischen 1 und 240 Minuten, weil Helium aufgrund seiner geringeren Molekülgröße deutlich höhere Diffusionsgeschwindigkeiten erreicht. He hat also im Durchschnitt eine um den Faktor 2.65 geringere Halbwertszeit im Körper als Stickstoff.

Werden 2 Inertgase verwendet (z. B. N ₂ und He als sog. "Trimix") ist der Inertgaspartialdruck für die einzelnen Gase erst gesondert auszurechnen und dann für das Gewebe zu addieren. In Visual Decompression wird folgende Funktion dafür verwendet

'Gewebepartialdrücke für Inertgas ausrechnen
Sub CalcPIOnTime(dblDepth#, dblTE#, dblN2Percent#, dblHePercent#)

Dim dblPiigN2#, dblPiigHe#
Dim T1&

For T1 = 1 To 16
    dblPiigN2 = (GetWaterPressure(dblDepth) - 0.063) * dblN2Percent / 100 'N2
    dblPiigHe = (GetWaterPressure(dblDepth) - 0.063) * dblHePercent / 100 'He
    dblPigTN2(T1) = dblPigTN2(T1) + (dblPiigN2 - dblPigTN2(T1)) * (1 - 2 ^ (-1 * dblDecoFactor * dblTE / dblTHalfN2(T1)))
    dblPigTHe(T1) = dblPigTHe(T1) + (dblPiigHe - dblPigTHe(T1)) * (1 - 2 ^ (-1 * dblDecoFactor * dblTE / dblTHalfHe(T1)))
    dblPigT(T1) = dblPigTN2(T1) + dblPigTHe(T1)
Next T1

End Sub

Die Summe der Inertgaspartialdrücke zur Zeit tE (Expositionszeit) errechnet sich also als Summe der einzelnen Inertgaspartialdrücke zum Zeitpunkt tE. Man muss also für eine Dekompressionsrechnung immer alle 16 Gewebe simultan und doch isoliert voneinander betrachten.

2.4.2 Auftauch-/Dekompressionsphase

Während der Dekompression (bzw. zu deren Beginn) beginnen die schnellen Gewebe bereits zu entsättigen, da der Umgebungsdruck und damit der inspiratorische Inertgaspartialdruck nachlassen, die langsamen sättigen fallweise noch weiter auf, da diese aufgrund ihrer langen Halbsättigungszeiten immer noch einen geringeren Inertgaspartialdruck aufweisen als er auf der Einatemseite vorliegt. Während dieser Phase wird logischerweise die in 2.4.1 gezeigte Sättigungsrechnung nicht beendet sondern weiter fortgeführt. Sie läuft die ganze Zeit auch während der Oberflächenpause.

Jetzt kommt allerdings eine zweite mathematische Betrachtung hinzu: Wenn der Inertgaspartialdruck eines Gewebes nach Gleichung (II) zur Zeit t _E und auf der Tauchtiefe berechnet wurde, muß nun für alle Gewebe eine weitere Gleichung angewendet werden, die den gerade tolerierten Umgebungsdruck (p.amb.tol) berechnet, bis zu dem aufgetaucht werden kann, ohne dass Gasblasen auftreten.

Diese Gleichung ist die für die eigentliche Dekompressionsphase relevante, sie lautet:

(III)

p _amb.tol : Von einem Gewebe noch tolerierter Druck, bei dem noch keine Gasblasen auftreten.
p _ig(tE) : Inertgaspartialdruck im Gewebe nach Expositionszeit t _E .
a, b : Die beiden verwendeten Faktoren a und b sind gewebespezifisch und stellen die mathematisch formulierte Toleranz des Gewebes gegen eine Übersättigung mit Inertgas dar. Der Faktor a ist dabei ein konstanter Druckwert in der Einheit [bar], der angibt, welchen absoluten Überdruck das Gewebe tolerieren kann, ohne dass sich freie Gasblasen bilden. b hat keine Einheit und gibt die Relation zwischen Umgebungsdruck und toleriertem Inertgaspartialdruck an. Es handelt sich folglich um den Linearfaktor einer Funktion ersten Grades der zum Ausdruck bringt, inweitet ein Gewebe bei einem bestimmten Umgebungsdruck eine definierte Gasüberspannung tolerieren kann.

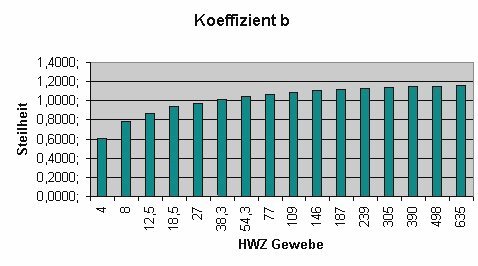
Die Koeffizienten für ZH-L16 sind:

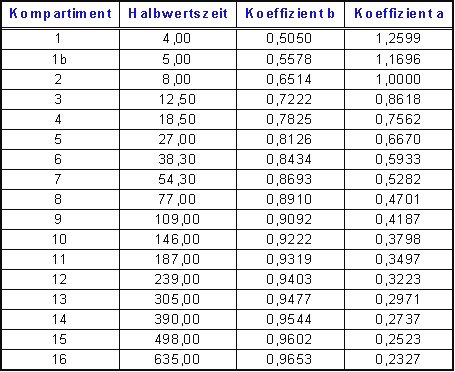
Berechnet werden Sie nach folgenden einfachen Formeln für das Modell ZH-L16:

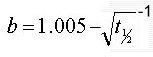
In das oben erwähnte Modell ZH-L12 sind die Werte für a- und b-Parameter als empirisch ermittelte Konstanten eingegangen, allerdings werden für die 16 Gewebe nur 12 verschiedene Zahlenpaare verwendet, in ZH-L16 sind sie funktional wie oben definiert.

Mathematisch betrachtet ist der symptomlos tolerierte Inertgasüberdruck eine lineare Funktion. Löst man Gl. III nach dem Inertgasüberdruck im Gewebe auf, so erhält man eine Geradengleichung für die gilt Steigung=1/b und Y-Achsenabschnitt=a:

p _ig(tE) = 1/b * p _amb.tol + a (IV)

Der Faktor a beschreibt dabei einen absoluten Überdruck, der immer toleriert wird, daher die Druckeinheit [bar]. b beschreibt dagegen eine lineare Beziehung von Umgebungsdruck => Tolerierter Inertgasüberdruck (p.amb => p.amb.tol). Anders formuliert: Je größer der Umgebungsdruck, desto größer wird der tolerierte Inertgasüberdruck.

Man erkennt hier übrigens die mathematischen Unsauberkeiten des Modells exemplarisch. a ist laut Bühlmann ein absoluter Druck, der immer toleriert wird. Die Einheit von a ist allerdings [bar]*[1/3.Wurzel aus min.] und nicht "bar".

Ähnliches lässt sich auch für b beobachten: Wenn b (bzw. dessen Reziprokwert b ^-1 ) wie dargelegt ein Steigungsfaktor ist, müsste er eine gebrochene Einheit aufweisen, da gilt m=Delta y/Delta x. Aus der Herleitung dieses Faktors ( b = 1,005 - t05 ^-1/2 ) ergibt sich allerdings die Einheit 1/(Wurzel aus min.) also min ^-1/2 . Die Konstante 1,005 ist dagegen einheitenlos. Desweiteren erkennt man den Kunstgriff Bühlmanns, zu verhindern, dass b jemals 0 wird. Die Konstante ist nämlich 1,005 und nicht 1,000, da sonst für ein Gewebe mit HWZ=1 min. b = 0 gelten würde. Nun gilt diese Bedingung für eine Gewebe mit der HWZ 0,9900745031064 min.

Da a und b wiederum Ergebnisse von Funktionen sind, liegt es nahe, diese graphisch darzustellen:

2.4.3 Die Ermittlung der Dekompressionsstufen

Um die gerade noch tolerierte Dekompressionstiefe zu errechnen, wird jeweils ermittelt, wann der Umgebungsdruck der nächsthöheren Deko-Stufe (also z. B. nach gängiger Stufung 3 m weniger Tauchtiefe als die aktuelle Dekompressionstufe) den von allen 16 Geweben höchsten noch tolerierten Umgebungsdruck gerade nicht unterschreitet. Dabei erfordert regelmäßig eines der Gewebe den höchsten noch einzuhaltenden Umgebungsdruck. Dieses jeweils "herausragende" Gewebe wird zum sog. "Führungsgewebe" und bestimmt, wie weit der Umgebungsdruck verringert werden kann. Es wird solange in der jeweiligen Dekompressionstiefe Tiefe verweilt, bis auf die nächste Dekompressionsstufe aufgetaucht werden kann, d. h. alle 16 Gewebe (genauer gesagt, das dann jeweils wirksame Führungsgewebe, das u. U. ein anderes sein kann als das der vorigen Stufe bzw. Zeitspanne) den dann verminderten Umgebungsdruck tolerieren können. Dabei schreitet die Entsättigung ständig fort, d. h. die Gasspannung in den Geweben wird kontinuierlich kleiner. Die Dekompressionsstufen folgen in modernen Austauchtabellen dann jeweils alle 3 m, was sich in der Praxis als angemessen erwiesen hat.

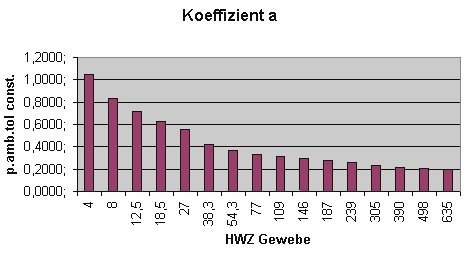
MIt weiter fortschreitender (Aus-)Tauchzeit wechselt das Führungsgewebe stetig. Während zu Beginn der Dekompression das Führungsgewebe unter den schnellen Geweben mit kurzen Halbwertszeiten zu finden ist, wird gegen Ende der Dekompression immer das jeweils nächstlangsamere Gewebe zum Führungsgewebe.

Zu den Toleranzgrenzen beim Trimix-Tauchen: Die Übersättigungstoleranzen der Gewebe (a- und b-Faktoren) sind für Stickstoff und Helium unterschiedlich. He hat geringere Halbwertszeiten als Stickstoff. Dadurch steigt die Gasspannung im Gewebe beim Aufsättigen schneller als bei einem langsam diffundierenden Gas. Auch wenn He den Körper schneller wieder verlassen kann und die Toleranzwerte gegen Übersättigung etwas höher sind als bei Stickstoff, wird aufgrund der deutlich erhöhten Gasspannung, die sich im Laufe der Sättigungsphase aufbaut, die Dekompressionsphase bei einem reinen He-O ₂-Gemisch länger dauern als bei einem TG mit Luft. Hier die Werte für die Toleranzen der Gewebe bei N ₂ und He:

' Stickstoff:

'a und b Koeffizienten N2
dblA_N2(1) = 1.2599: dblB_N2(1) = 0.505
dblA_N2(2) = 1.0000: dblB_N2(2) = 0.6514
dblA_N2(3) = 0.8618: dblB_N2(3) = 0.7222
dblA_N2(4) = 0.7562: dblB_N2(4) = 0.7725
dblA_N2(5) = 0.6667: dblB_N2(5) = 0.8126
dblA_N2(6) = 0.5933: dblB_N2(6) = 0.8434
dblA_N2(7) = 0.5282: dblB_N2(7) = 0.8693
dblA_N2(8) = 0.4701: dblB_N2(8) = 0.891
dblA_N2(9) = 0.4187: dblB_N2(9) = 0.9092
dblA_N2(10) = 0.3798: dblB_N2(10) = 0.9222
dblA_N2(11) = 0.3497: dblB_N2(11) = 0.9319
dblA_N2(12) = 0.3223: dblB_N2(12) = 0.9403
dblA_N2(13) = 0.2971: dblB_N2(13) = 0.9477
dblA_N2(14) = 0.2737: dblB_N2(14) = 0.9544
dblA_N2(15) = 0.2533: dblB_N2(15) = 0.9602
dblA_N2(16) = 0.2327: dblB_N2(16) = 0.9653

' Helium:

'a und b Koeffizienten He
dblA_He(1) = 1.7424: dblB_He(1) = 0.4245
dblA_He(2) = 1.383: dblB_He(2) = 0.5747
dblA_He(3) = 1.1919: dblB_He(3) = 0.6527
dblA_He(4) = 1.0458: dblB_He(4) = 0.7223
dblA_He(5) = 0.922: dblB_He(5) = 0.7582
dblA_He(6) = 0.8205: dblB_He(6) = 0.7957
dblA_He(7) = 0.7305: dblB_He(7) = 0.8279
dblA_He(8) = 0.6502: dblB_He(8) = 0.8553
dblA_He(9) = 0.595: dblB_He(9) = 0.8757
dblA_He(10) = 0.5545: dblB_He(10) = 0.8903
dblA_He(11) = 0.5333: dblB_He(11) = 0.8997
dblA_He(12) = 0.5189: dblB_He(12) = 0.9073
dblA_He(13) = 0.5181: dblB_He(13) = 0.9122
dblA_He(14) = 0.5176: dblB_He(14) = 0.9171
dblA_He(15) = 0.5172: dblB_He(15) = 0.9217
dblA_He(16) = 0.5119: dblB_He(16) = 0.9267

Die Ermittlung der a- und b-Faktoren bei Inertgasgemischen aus N ₂ und He geschieht über eine einfache Gewichtung der einzelnen Inertgasanteile im Atemgas. Bei der Berechnung der Dekompression werden diese Werte gelesen und in Relation zum momentanen Gewebeinertgaspartialdruck gesetzt:

' Berechnen des Umgebungsdruckes, bei dem gerade noch keine
' Gasblasen auftreten
Function GetAmbTolPressure#(lngFN2&, lngFHe&)

Dim T1&, a#, b#
Dim dblPambTol#, dblMaxP#
Dim dblFN2#, dblFHe#

dblMaxP = 0
dblFN2 = lngFN2 / 100 + 0.001
dblFHe = lngFHe / 100 + 0.001

For T1 = 1 To 16
    a = (dblA_N2(T1) * dblFN2 + dblA_He(T1) * dblFHe) / (dblFN2 + dblFHe)
    b = (dblB_N2(T1) * dblFN2 + dblB_He(T1) * dblFHe) / (dblFN2 + dblFHe)
    dblPambTol = (dblPigT(T1) - a) * b
    If dblPambTol > dblMaxP Then
      dblMaxP = dblPambTol
    End If
Next T1

GetAmbTolPressure = dblMaxP

End Function

Diskussion: Muss die Dekompressionsrechnung immer in Form einer Iteration erfolgen?

Wie hier gezeigt wird, ist ein iterativer Ansatz relativ leicht in einem Computerprogramm zu implementieren. Wenn genug Rechenleistung zur Verfügung steht ist dies sicher immer eine tragfähige Lösung, zumindest für PC-basierte Dekompressionsprogramme. Glücklicherweise haben moderne Mikrocontroller in Verbindung mit modernen Compilern zwar gute Fähigkeiten in Gleitkommarithmetik, es kann aber u. U. sein, dass die Rechenleistung beilangen Dekompressionszeiten und einer hohen Gewebezahl doch relativ lange ausfallen. In diesem Falle läge es nahe, nicht eine Iteration zu programmieren sondern die Gleichungen entsprechnd umzuformen und die Expositionszeit auf einer gegebenen Dekompressionsstufe, die nötig ist, um regelgerecht zu dekomprimieren, direkt zu berechnen. Es sind hierbei zwar infolge der Gewebezahl auch noch iterative Elemente erforderlich, sie werden jedoch weniger relevant da die Hauptrechenarbeit wegfällt.

Folgender Ansatz führt theoretisch zu einer weitgehend iterationsfreien Lösung:

Einsetzen von Gl. II in III
Logartihmieren der Gleichung und Auflösen nach der Expositionszeit

Wie dabei genau vorzugehen ist, steht weiter unten zu lesen, denn bei der Berechnung der Nullzeit wird dieses Verfahren angewandt. Da aber fallweise Konstellationen denkbar sind, die dazu führen, dass die Gleichungen in der logarithmierten Form nicht (oder nicht eindeutig) lösbar sind, stellt dieses Verfahren keinen universell anwendbaren Ersatz für die Iteration dar. Leider.

2.5 Die Berechnung der Nullzeit

Auch die Berechnung der sog. Nullzeit , also die Zeit, bis zu der man bei einer bestimmten Auftauchgeschwindigkeit bis zur Oberfläche (i. e. ca. 1 bar Umgebungsdruck) austauchen kann ohne dabei Dekompressionstopps einhalten zu müssen, kann man mit dem Bühlmannmodell vorgenommen werden.

Selbstredend könnte man die Berechnung der Nullzeit für eine gegebene Situation (Gewebesättigung, inpiratorischer Inertgaspartialdruck) auch iterativ (mit einer Schleifenberechnung) lösen. Eleganter geht es allerdings, wenn man die Mathematik des Bühlmannmodells zugrunde legt und sich der in den Gleichungen enthaltenen Definitionen bedient. Wir gehen dabei davon aus, dass die Expositionszeit so berechnet werden kann, dass, wenn man als p.amb.tol aus Gl III den Umgebungsdruck an der Oberfläche (i. e. den Luftdruck) einsetzt, die kürzeste Nullzeit aller 16 Gewebe das gesuchte Rechenergbenis sein wird.

Zuerst wird also Gleichung III nach p.i.g (Inertgaspartialdruck, i. e. Sättigungszustand des Gewebes) umgeformt:

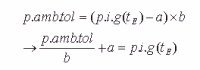
Anschließend werden beide Gleichungen gleichgesetzt (ab der 2. Zeile in unten stehender Herleitung) und nach der Expositionszeit tE aufgelöst. Dazu verwendet man einen Logarithmus. da gilt log(n ^x ) = x * log(n) . Dieser Logarithmus wird später dann leider allerdings zum Stolperstein in besonderen Fällen (siehe unten).

Zuerst schreibt man die Sättigunsgleichung (1. Zeile), dann folgt durch Gleichsetzen von der oben aufgelösten Gl III und Umformen bzw. Auflösen nach t _E

Nach dem oben vorgenommenen beidseitigen Logarithmieren und weiterem Umformen ergibt sich:

tE wird dann:

Diese dargestellte Rechnung wird auf alle 16 Gewebe angewandt, die kürzeste Nullzeit bestimmt die Gesamtnullzeit. Am besten bindet man diese Gleichung softwaretechnisch in eine Schleifenstruktur ein:

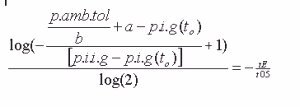
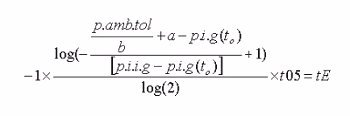
int calc_ndt()
{
int dp; /* Wassertiefe in m */
int t1, t0min = 999;
float piigN2, te, x, airpressure = 1.001; /* airpressure: Luftdruck in bar */

for(t1 = 0; t1 < 16; t1++)
{
    piigN2 = (dp / 10 + airpressure - 0.0627) * FN2;
    x = -1 * (((airp / bN2[t1] + aN2[t1] - piN2[t1]) / (piigN2 - piN2[t1])) - 1);
    if(x > 0)
    {
      te = -1 * log(x) / log(2) * t05N2[t1];
      if(te < t0min)
        t0min = te;
    }
}
return t0min;
}

Ein Problem stellt sich dabei, wie bereits vorstehend kurz angedeutet, in Zusammenhang mit Nullzeiten in geringen Tiefen (unter 10 m) bzw. unter bestimmten Sättigungszuständen (p.i.g). Abhängig von den Gegebenheiten wird der Ausdruck im Argument des Logarithmus des Zählers fallweise negativ, d. h. eine Nullzeitenberechnung ist für diese Fälle nicht möglich.

Peter Rachow 2004