![]()
![]()
Forschung und Entwicklung: LCD-Anzeige | Mikrocontroller | Software | Sensoren | Gehäuse | Erfahrungsberichte
![]()
Drucksensoren arbeiten üblicherweise entweder als Absolut - oder als Relativdrucksensoren . Für unsere Anwendungen als Druckmesser in Tauchcomputern weitaus besser geeignet sind die Absolutdrucksensoren. Sie benötigen keinen Druckunterschied zwischen 2 verschiedenen Seiten des Sensor und lassen sich daher idealerweise vollständig vom zu messenden Medium umgeben. Da jedoch Wasser (insb. Salzwasser) den Sensoren schaden, also z. B. die Anschlüsse oder das Messsubstrat korrodieren lassen bzw. durch seine Leitfähigkeit die Messbrücke stören würde, ist es erforderlich, den Sensor in eine separate Kammer einzubauen, die mit einem Schutzmedium (z. B. Silikonöl) gefüllt ist und mit dem Umgebungswasser über eine flexible Membrane mit Druck beaufschlagt werden kann. Diese Notwendigkeit entfällt bei der Verwendung von sog. gelgeschützten Sensoren, die bereits mit einem Schutzgel gegen aggressive Agenzien geschützt sind. Über den Einbau eines ungeschützten Sensors in ein Gehäuse bzw. eine vorstehend erwähnte ölgefüllte Sensorkammer gibt Kapitel 5 Auskunft.
Relativdrucksensoren vergleichen im Gegenzug zu dem vorher besprochenen Sensortyp zwei Drücke, die von verschiedenen Seiten an das System angreifen. Sie sind u. U. dann verwendbar, wenn das Gehäuse des SBTC einen konstanten Innendruck entsprechend dem Äquivalent des Oberflächenluftdrucks aufweist. Wer aber die Möglichkeit hat, auf einen Absolutdrucksensor zuzugreifen, ist damit besser weitaus beraten.
Um die Druckwerterfassung mit Sensoren zu realiseren gibt es nun verschiedene Möglichkeiten basierend auf verschiedenen Technologien:
| Bestimmte miteinander in mechanischen Kontakt gebrachte Halbleiter wie z. B. Kohle- oder Graphitstäbe verändern den Übergangswiderstand zwischen den einzelnen Teilen des Systems mit dem Druck, der auf den Komponenten lastet. Dieser Sachverhalt ist z. B. von den sog. Kohlemikrofonen bekannt. Also begann ich, testweise einen einfachen Sensor zu konstruieren. Er besteht aus einem Kohlestab, an den zwei Graphitstäbe (Bleistiftminen) parallel angelagert sind. Das Ganze sitzt in einem Röhrchen aus Schrumpfschlauch und ist wasserdicht verpackt: |
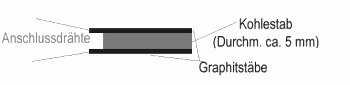 Bild 1a: Einfachsensor auf Kohle-Graphitbasis zu Experimientierzwecken |
Erste Versuche ergaben zusammenfassend folgendes Ergebnis: Das System erkennt mechanische Drücke zwischen 0 und ca. 1 bar Überdruck und setzt sie in eine Widerstandsänderung um. Diese ist natürlich von ihrer Reproduzierbarkeit her nicht exakt, d. h. es entsteht weder eine linear vom Druck abhängige noch eine reproduzierbare Ausgangsgröße. Daher dient der Aufbau nur der grundsätzlichen Exploration des Aufbaus und der Wirkungsweise von Drucksensoren. Ein interessantes Experiment, mehr nicht.
| Die
Firma Conrad
electronic hat Foliensensoren im Programm. die laut Katalog als
Druckschalter
dienen können.
Diese
Bauteile
setzen einen Druck zwischen 0 und 10 bar Überdruck in einen
elektrischen
Widerstand im Bereich von knapp unterhalb unendlich (R >
> ca. 10 M |
 Bild 1b: Conrad Folienssensoren (Foto: Conrad electronic) |
| Zuerst
legte ich
dazu den Foliensensor, den es bei Conrad zu ca. 6 Euro/Stück gibt ,
auf ein Stückchen Alublech (20 x 80 x 2 mm) und klebte ihn dort
mit
2-Komponentenkleber (UHU plus) an. Dann setzte ich ein Alu-Rohr mit dem
Durchmesser 10 mm und der Länge 5 cm auf die Sensorfläche auf
und dichtete am Übergang zum Foliensensor bzw. zur
Grundfläche
ringförmig ebenfalls mit UHU plus ab. An dieses Alurohr wird
später
mit einem Druckschlauch den Mitteldruckabgang (MD) der ersten Stufe
eines
Atemreglers angeschlossen, um bis zu 10 bar Prüfdruck auf den
Sensor
zu geben. Endziel ist dabei die Aufnahme einer Druck-Widerstandskurve.
Dieses Gerät wird wie beschrieben mit dem offenen Ende des Alu-Rohres an die erste Stufe eines Atemreglers (AR) angeschlossen umd die Anordnung dosiert unter Druck setzen zu können. Dazu verwende ich einen alten zerschnittenen AR-Mitteldruckschlauch, den ich mit einem handelsüblichen Druckluftschlauch aus dem Baumarkt zusammengekoppelt habe. Alle Schläuche werden mit kleinen Schlauchschellen und den im Baumarkt in der Abteilung "Druckluft" zu erwerbenden Rohrverbindern gut verbunden. Zusätzlich befindet an der 1. Stufe des Atemreglers ein Druckmesser bis ca. 15 bar, z. B. ein Kompressionsdruckprüfer für Verbrennungsmotoren oder ein handelsübliches Mitteldruckmanometer aus dem Werkzeughandel, um den im System enthaltenen Luftdruck genau ablesen zu können. |
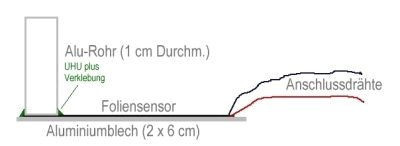 Bild 2: Versuchsaufbau mit Conrtad-Foliensensor |
|
|
Wie man sehr leicht erkennen kann, handelt es sich um eine Funktion vom Typ f(x) = k * x -n . Für unsere Zwecke ist diese nicht brauchbar, da im Bereich von p.amb > = 2 bar, aus einer Druckänderung nur eine sehr kleine Widerstandsänderung folgt. Die Ergebnisse wären also von der Genauigkeit und Reproduzierbarkeit vermutlich nicht akzeptabel.
Beenden wir nun diese Experimente und wenden uns den Produkten der Industrie zu..
Von einem
Freund
bekam ich einen alten elektronischen Tiefenmesser geschenkt, der einen
Drucksensor der Firma Siemens enthielt. Dieser Sensor (Siemens
KPY14
(=Infineon
KPY45A
)) wird heute noch im Internet vereinzelt angeboten,
obwohl er beim Hersteller (Siemens bzw. Infineon) bereits lange
ausgelaufen
ist.
| Die
Daten dieses
Bauteils (Siemens KPY14 =Infineon KPY45A) sind auszugsweise laut Datenblatt
:
p Betrieb
=
0...10 bar Überdruck Ferner enthält der Sensor einen temperaturabhängigen Widerstand, über den eine später zu definierende Temperaturkompensation angesteuert werden kann. Hinweis: Es wird im folgenden Text was die Druckeinheit betrifft, folgendermaßen verfahren: Es wird, wenn von Druck gesprochen wird. dieser Druck in der Einheit [bar Überdruck] angegeben, wie er auch einem Manometer abzulesen ist. Der zusätzlich hinzuzurechnende Luftdruck fällt dabei aus der Betrachtung heraus. 5 bar Überdruck entsprechen einem Gesamtdruck von 5 bar Wasserdruck + ca. 1 bar Luftdruck = ein absoluter Umgebungsdruck von 6 bar. Der Sensor benutzt, wie alle unkompensierten analogen Drucksensoren, vier auf Piezobasis arbeitende resistive Druckelemente (druckabhängige Widerstände), die zu einer sog. Wheatstoneschen Brücke zusammengeschaltet sind. Eine Messbrücke nach dem Wheatstone-Prinzip ergibt eine Ausgangsspannung (V out ) von 0V wenn alle Widerstände den gleichen Wert haben (=Nullzustand). Verändert sich ein Widerstand leicht, führt dies bereits zu einer relativ großen Änderung der Ausgangsspanung. Diese Messbrückenschaltung ist also gut geeignet, kleine Widerstandänderungen in große Spannungsänderungen umzusetzen. Die einzelnen Widerstände dieser Drucksensorbrücke sind dabei so angeordnet, dass bei Druckbeaufschlagung jeweils zwei einander gegenüberliegende Elemente ihren Widerstandswert gegensinnig verändern und das daraus resuliterende Ungleichgewicht der Brücke (und damit die Ausgangsspannung V out ) maximiert wird. Zum besseren Verständnis der Schaltung des Sensors rechts der Auszug aus dem Datenblatt. |
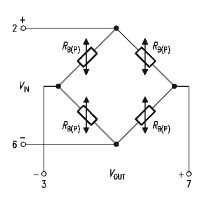 Bild 4a: Innenschaltung des Sensors KPY 14 Erläuterung: V IN ist die Eingangspannung, die später (im Tauchcomputer) stabilisiert sein muss, V OUT ist die druckabhängige Ausgangsspannung. |
Die Wheatstone-Brücke ist ohne externe Baulemente (Abgleichwiderstand) i. d. R. bei Umgebungsdrcuk (p.amb) = 0 bar nicht vollständig im Gleichgewicht. Daher benötigt man noch eine
So sieht die entsprechende Schaltung in der Endversion aus:
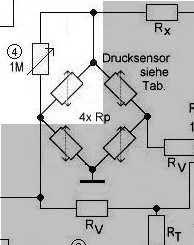
Bild 4b Die Nullpunktjustierung
mit Trimmer 1M
![]() (4)
(4)
In der Praxis wird man den Trimmerwiderstand durch Probieren grob ermitteln. Dann benutzt man ein Potentiometer, dessen Wert geringer ist und schaltet einen Festwiderstand in Reihe. Dadurch lässt sich die Nullpunktjustierung feiner vornehmen.
Anschließend
kann man zur Orientierung über die Ausgangsgröße des
Sensors
die Druck-Spannungskurve aufnehmen. Mit meiner oben beschriebenen
Versuchsanordnung
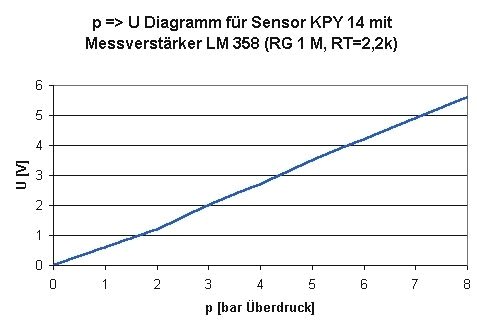
konnte ich folgende p => U-Funktion ermitteln:
T = 25°C (Anmerkung: DerSensor erfordert eine Temperaturkompensation) |
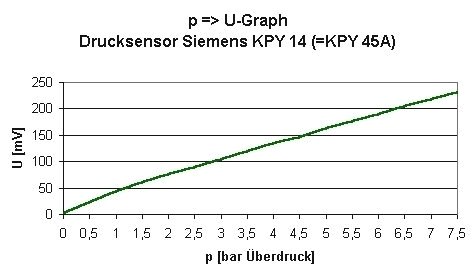 Bild 5: p => U-Kurve des Sensors KPY 14 |
Die Linearität scheint für den Anwendungszweck ausreichend. Nachfolgend ermittelt man der Vollständigkeit halber die Funktionsgleichung. Sie ist von der Struktur
U = mp + b (I)
Geht man davon aus, dass gilt m = dy/dx so erhält man aus obiger Tabelle als Mittelwert der Steigungen im Bereich von p = 2..6 bar den Wert m = 30. Es ergibt sich daher folgende Funktionsgleichung
U = 30 * p + b (II)
Allerdings wird diese Funktionsgleichung des gesamten Druckerfassungssystems durch den nachfolgenden beschriebenen (und erforderlichen) Messverstärker anders ausfallen (veränderter Steigunsfaktor m), aber als mathematische Überlegung ist sie immerhin nicht uninteressant, zumal später beim Temperatursensor eine derartige Funktion benötigt werden wird.
Eine derartige Aufgabenstellung lässt sich am besten mit einem Operationsverstärker (OP) lösen. Dabei handelt es sich, kurz gesagt, um einen Baustein, dessen Eingangstufe ein sog. Differenzverstärker ist, ein Verstärker mit zwei Eingängen also, an denen jeweils eine Spannung angelegt wird und man als Verstärkungsergebnis ein Vielfaches (bis zum Faktor 10 6 ) der Differenz dieser beiden Spannungen erhält. Für unser spezielles Problem sieht die Lösung passenderweise so aus, dass wir die beiden Leitungen von V out des Drucksensors auf je einen der beiden Eingänge eines OP geben und als Ergebnis die verstärkte Spannungsdifferenz (und damit letztlich eine Umsetzung des angelegten Druckes) erhalten.
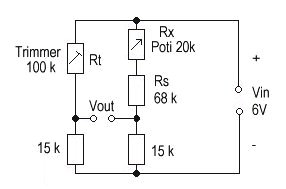
Bild 6: Hilfsschaltung
zur Simulation des Drucksensors KPY 14 für Testzwecke
Erläuterung
der Schaltung:
Mit dem Trimmer 100 k
![]() wird die
Brücke auf 0 V für V
out
eingestellt. MIt
R
x
lässt sich dann die Spannung V
out
zwischen
0 und einem Endwert verändern (Simulation des Drucksensors). R
s
verringert dabei die Wirksamkeit von R
x
und sollte so bemessen
sein, dass ein vollständiges Überstreichen der Schleifbahn
von
R
x
(von Anschlag zu Anschlag) in einer Spannungsänderung
von ca. 0...0.3 V resultiert, was dem Spannungsintervall des hier
ntersuchten
Drucksensors KPY14 zwischen 0 bar Überdruck und max.
Überdruck
entspricht. Damit wird der Drucksensor sehr einfach simuliert und man
kann
sich den nachfolgenden Aufgaben widmen.
wird die
Brücke auf 0 V für V
out
eingestellt. MIt
R
x
lässt sich dann die Spannung V
out
zwischen
0 und einem Endwert verändern (Simulation des Drucksensors). R
s
verringert dabei die Wirksamkeit von R
x
und sollte so bemessen
sein, dass ein vollständiges Überstreichen der Schleifbahn
von
R
x
(von Anschlag zu Anschlag) in einer Spannungsänderung
von ca. 0...0.3 V resultiert, was dem Spannungsintervall des hier
ntersuchten
Drucksensors KPY14 zwischen 0 bar Überdruck und max.
Überdruck
entspricht. Damit wird der Drucksensor sehr einfach simuliert und man
kann
sich den nachfolgenden Aufgaben widmen.
Hier der Schaltplan, allerdings ohne die Messbrücke vollständig darzustellen, die Nullpunktjustierung der Brücke wurde der Einfachheit weggelassen.:
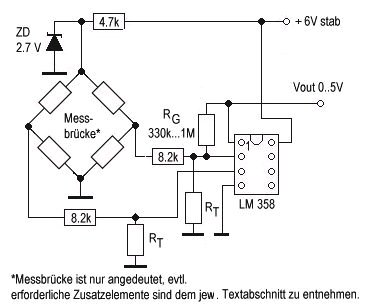
Bild 7: Prinzipschaltung
eines Messverstärkers für den Sensor KPY 14
Erläuterungen zum Schaltplan:
| Sensorbezeichnung | R1 | RT | RG |
| Siemens KPY 14 (10-bar Sensor) | 8,2k | 8,2k | 1M |
| Intersema MS5212 BZ (12-bar Sensor) | 8,2k | 1,0k | 1M |
| SenSym 13 U 0500 PA 0 K (34-bar Sensor = 5000 psi) | 2,7k | --- | 1M |
Ist die Schaltung aufgebaut und unter Zuhilfenahme der Simulatorschaltung auf grundsätzliche Funktion überprüft, beginnt
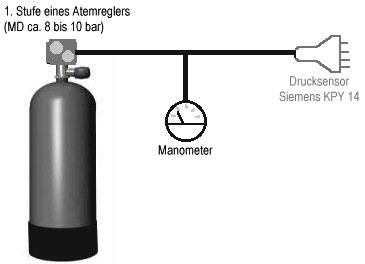
Bild 8: Einmessvorrichtung
zur Druckbeaufschlagung des Sensors mit Druckluft
Der Druck aus dem Atemregler wird zu Beginn des Versuches auf 8 bar eingestellt, das Ventil der Flasche wird dann geschlossen und während der Aufnahme einer Messreihe mit der Luftdusche der ebenfalls noch angeschlossenen (oben aber nicht gezeigten) zweiten Stufe bei geschlossenem Flaschenventil kontinuierlich vermindert.
Die Versuche, die nun durchgeführt werden dienen dazu, zu überprüfen, ob die Spannung, die der Messverstärker abgibt, in einer linearen Abhängigkeit zum auf den Sensor gegebenen Druck steht. Eine (fast optimale) Kurve, die am Ende der Versuchsreihe stehen sollte, sieht in etwa so aus:
Folgendes Vorgehen kommt dabei zur Anwendung:
a) Aufnahme einer
Druck-Spannungskurve für z. B. alle ganzzahligen Druckwerte
zwischen
0 und 8 bar Überdruck und Anlegen einer Wertetabelle.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b) Auswertung
der
Wertetabelle mit grafischen Werkzeugen (z. B. Excel) in Hinblick auf
Linearität
der Druck-Spannungs-Funktion (p => U)
c) Korrektur der
Verstärkerparametrierung mit dem Ziel der Optimierung der
Linearität
(siehe unten Abschnitt 2.2.4)
d) Start des nächsten
Versuches.
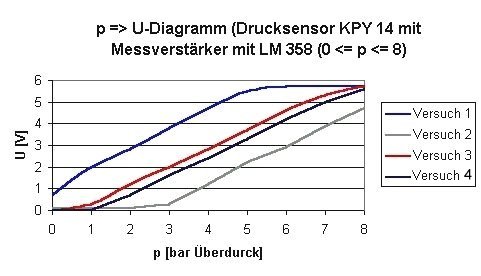
Bild 10: Messkurven
mit verschiedenen Einstellungen für die Arbeitspunkteinstellung
des
Sensors
Das Ergebnis einer suboptimalen Kurve wird i. d. R. so aussehen wie in obiger Grafik (im Extremfalle) "Versuch 1" oder "Versuch 2". In weniger gravierenden Fällen wie "Versuch 3" bzw. "Reihe1", die beide am unteren Ende noch leicht unlinear sind. Diese Verzerrungen sind ein Indiz, dass der Messverstärker in den Grenzbereichen (i. e. geringe oder max. Aussteuerung) noch nicht im optimalen Arbeitspunktbereich oder bereits in der Sättigung betrieben wird. Die Ursache ist eine zu geringe oder eine zu hohe Spannung am Verstärkereingang bzw. letztllich ein zu großer "Swing"-Bereich des Sensors (Amplitude), d. h. die Sensorspannung (bzw. deren Extremwerte) passt nicht in das linear zu verstärkende Intervall des OP.
Ursache des Problems:
Der OP hat, wie jeder andere Verstärker auch, nur einen bestimmten Eingangsbereich, in welchem eine Eingangsgröße (Spannung bzw. Stromstärke, je nach Verstärkertyp) linear in eine Ausgangsgröße (Spannung bzw. Stromstärke) überführt wird. Verlässt man diesen Bereich, so ist die Funktion der Ausgangsspannunng nicht mehr linear, es kommt zu Verzerrungen.
Ein Beispiel: Ein Verstärker habe folgende Eingangs-Ausgangsrelation:
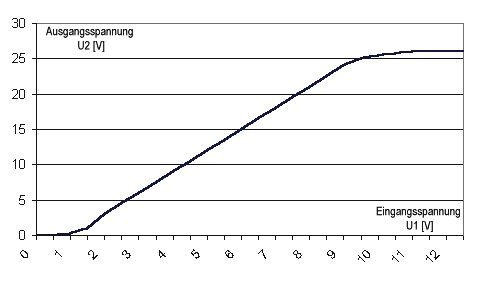
Bild 11: Verstärkerkennlinie
U
Ein
=> U
Aus
eines realen Verstärkers
Man erkennt, dass eine verhältnisrichtige (lineare) Umsetzung der Eingangsspannung in eine verstärkte Ausgangsspannung nur im Bereich 2 V <= U1 <= 9 V erfolgt. Spannungen die kleiner oder größer sind werden nicht linear umgesetzt, d. h. das Verhältnis U1/U2 ist nicht konstant.
Die Lösung dieses Problems:
Wenn die Linearität des Messverstärkers optimiert ist, sind noch einige Abschlussarbeiten erforderlich, bevor die Sensorik im SBTC zum Einsatz kommen kann:
Dies ist zuvorderst
die Ergänzung der Messverstärkerschaltung auf den in Bild 12
gezeigten Stand. Hinzu kommen z. B. einige Glättungskondesatoren
(10uF)
am Ausgang des Messverstärkers bzw. 100uF-Kondensatoren in
der
Plusleitung und dort ebenfalls ein 100
![]() -Widerstand.
Sinn dieser Elemente ist es, die kurzfristige Fehlanzeigen der
Messschaltung
(z. B. durch nie vollständig zu elimierende
Betriebsspannungsschwankungen)
zu minimieren.
-Widerstand.
Sinn dieser Elemente ist es, die kurzfristige Fehlanzeigen der
Messschaltung
(z. B. durch nie vollständig zu elimierende
Betriebsspannungsschwankungen)
zu minimieren.
Weiterhin wichtig
ist vor allem die genaue Einstellung der
Verstärkerausgangsspannung
um später einen bestimmten Tiefenwert (Meter Wassertiefe) zur
Anzeige
zu bringen: Der Ausgang des LM 358 wird dazu an ein Ende eines 10k
![]() -Trimmers,
dessen anderes Ende auf Masse liegt, angeschlossen (s. u. stehende
Grafik).
Am Schleifer des Trimmers lässt sich dann eine geteilte Spannung
abgreifen,
die so justiert wird, dass z. B. 80m Wassertiefe (= ca. 8 bar
Überdruck)
einer Spannung von 3,90625 V entsprechen. Dieses Vorgehen basiert
auf der Anwendung eines 10 bar (Überdruck) Sensors, bei dem 102.4
m
WT
(i.e. eine Auflösung von 0.1 m Wassertiefe und 1024
AD-Wandlerschritten) einer Spannung von 5 V entspricht, d. h. eine
Spannung
pro
Meter Wassertiefe (m
WT
) von 102.4m
WT
/ 5V =
20,48 m
WT
/V, was in der Umkehrrelation 0,04882V/m
WT
ergibt.
-Trimmers,
dessen anderes Ende auf Masse liegt, angeschlossen (s. u. stehende
Grafik).
Am Schleifer des Trimmers lässt sich dann eine geteilte Spannung
abgreifen,
die so justiert wird, dass z. B. 80m Wassertiefe (= ca. 8 bar
Überdruck)
einer Spannung von 3,90625 V entsprechen. Dieses Vorgehen basiert
auf der Anwendung eines 10 bar (Überdruck) Sensors, bei dem 102.4
m
WT
(i.e. eine Auflösung von 0.1 m Wassertiefe und 1024
AD-Wandlerschritten) einer Spannung von 5 V entspricht, d. h. eine
Spannung
pro
Meter Wassertiefe (m
WT
) von 102.4m
WT
/ 5V =
20,48 m
WT
/V, was in der Umkehrrelation 0,04882V/m
WT
ergibt.
Hier nun noch einmal abschließend die vollständige Schaltung der Drucksensorik mit allen Bauteilen:
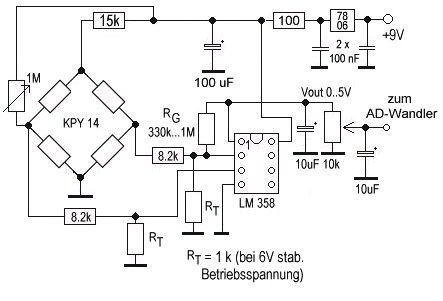
Bild 12: Schaltung
des Messverstärkers
Zuerst
empfiehlt
es sich, den Minimalwert am Potentiometer (Trimmerwiderstand) 10k
![]() so zu
justieren, dass die Tiefenanzeige bei völlig druckentlastetem
Sensor
00.0m
anzeigt. Dann stellt man einen Druck von 8 bis 10 bar
Überdruck ein und justiert mit dem 1M
so zu
justieren, dass die Tiefenanzeige bei völlig druckentlastetem
Sensor
00.0m
anzeigt. Dann stellt man einen Druck von 8 bis 10 bar
Überdruck ein und justiert mit dem 1M
![]() -Poti
an der Sensorbrücke auf den druckäquivalenten maximalen
Tiefenwert
von z. B. 80m (entspr. 8 bar Überdruck). Daraufhin vermindert man
den Druck auf die Hälfte und regelt nochmals den 1M
-Poti
an der Sensorbrücke auf den druckäquivalenten maximalen
Tiefenwert
von z. B. 80m (entspr. 8 bar Überdruck). Daraufhin vermindert man
den Druck auf die Hälfte und regelt nochmals den 1M
![]() -Trimmer
nach bis die Tiefenangabe korrekt zum Druckwert passt. Bei meinem
Versuchsaufbau
ergab sich dadurch während der Überprüfung auf der
ganzen
Tiefenskala von 0 bis 80m eine Tiefenabweichung vom Sollwert von max.
+/-0.2m.
-Trimmer
nach bis die Tiefenangabe korrekt zum Druckwert passt. Bei meinem
Versuchsaufbau
ergab sich dadurch während der Überprüfung auf der
ganzen
Tiefenskala von 0 bis 80m eine Tiefenabweichung vom Sollwert von max.
+/-0.2m.
Inwieweit hier
bereits Unlinearitäten des Manometers bzw. Ableseungenaugkeiten
einwirken,
kann ich mangels quantitativer Informationen nicht sagen. Aber
insgesamt
kann man wohl konstatieren, dass die Tiefenazeige bei konstanter
Temperatur
vergleichsweise genau arbeitet.
 Bild 13: Der Messaufbau zur Druckbeaufschlagung des Sensors mit SBTC (Version 1, hier nicht mehr beschrieben). Links oben der Drucksensor am Mitteldruckabgang eines Atemreglers |
Der
SBTC wird
dazu in ein Wasserbad gelegt, dessen Temperatur von einer
Anfangstemperatur
(z. B. +5°C) schrittweise auf einen Endwert (z. B. +40°C)
gebracht
wird. Der Sensor wird mit einem gleichbleibenden Druck beaufschlagt.
Dann
werden jeweils nach einer bestimmten Zeit des Temepraturausgleichs
(mindestens
10 min.) folgende Werte bestimmt:
|
 Bild 14: SBTC (Version 1) im Kaltwasserbad |
Man erhält
nach dem Versuch eine Tabelle ähnlich dieser
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Wie sich erkennen lässt ist die Tiefenanzeige funktional abhängig von der Umgebungstemperatur. Man erhält im Bereich DeltaT von 20K einen Tiefenunterschied von 0,9 m Wassertiefe.
Für meine Versuche standen mir je ein PTC- und ein NTC-Widerstand zur Verfügung. Das PTC-Element ist ein handelsüblicher Sensor mit der Typbezeichung KTY18. Über die Einsatzfähigkeit dieser Bauteile als Tempratursensor gab ein Versuch Auskunft. Es sollte ein T=> R-Diagramm erfasst werden, um die qualitative und quantitative Umsetzung des Temperaturwertes in eine elektrische Größe (in diesem Falle den elektrischen Widerstand) zu analysieren.
Es ergaben sich
folgende Kurven als Ergebnis:
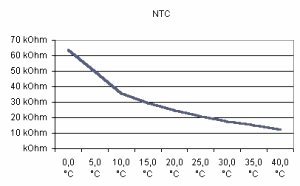 Bild15: T => R-Diagramm NTC |
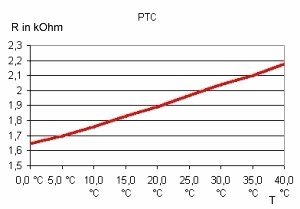 Bild16: T => R-Diagramm PTC |
Interpretation:
Man erkennt, dass der NTC-Widerstand eine Temperatur->
Widerstandskurve
erzeugt, die exponenziellen Charakter aufweist und gegen einen Endwert
< 1 k
![]() approximiert.
Diese Kurve ist softwaretechnisch schwieriger auszuwerten als die
lineare
Kurve des PTC-Elementes. Die Wahl fällt daher auf letzteres.
approximiert.
Diese Kurve ist softwaretechnisch schwieriger auszuwerten als die
lineare
Kurve des PTC-Elementes. Die Wahl fällt daher auf letzteres.
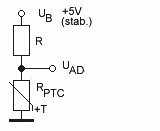
Bild 17: Spannungsteiler
mit PTC
U R / U PTC = R / R PTC
=> (U B - U AD ) / U AD = R / R PTC (IV)
Steigt also der
Widerstandswert von R
PTC
, weil die Temperatur steigt, wird
auch die Spannung U
AD
proportional anwachsen. Der Wert von R
wird so bestimmt, dass bei einer Temperatur von 20°C die Spannung U
AD
ca.
die Hälfte von U
B
ist, daher werden R und R
PTC
in
etwa gleich groß sein. Aus dem Diagramm lesen wir für
T=20°C
einen Widerstandswert won R
PTC
=1.9k
![]() ab. Dieser
Widerstandswert muss genau eingehalten werden, um die Temperaturmessung
exakt durchzuführen. Ggf. kann der Wert durch Reihenschaltung
eines
1.8k
ab. Dieser
Widerstandswert muss genau eingehalten werden, um die Temperaturmessung
exakt durchzuführen. Ggf. kann der Wert durch Reihenschaltung
eines
1.8k
![]() - und eines
100
- und eines
100
![]() -Widerstandes
dargestellt werden.
-Widerstandes
dargestellt werden.
R = m * T + b
| Temperatur T | R PTC | m = dy/dx |
| 30 | 2000 | |
| 35 | 2100 | 20 |
| 40 | 2200 | 20 |
Da für die
Steigung m einer linearen Funktion gilt
m = dy/dx = (y
1
-y
0
)
/ (x
1
-x
0
)
, erhält man für jedes
Wertepaar einen Steigungsfaktor m. Aus allen Werten für m wird der
Durchschnitt gebildet (m= 0,02 k /K).
/K).
Den y-Achsenabschnitt
b
erhält man aus dem Wert für T = 0°C: 1,7k
![]() .
Es gilt also für den hier untersuchten Temperatursensor folgende
Funktionsgleichung:
.
Es gilt also für den hier untersuchten Temperatursensor folgende
Funktionsgleichung:
R PTC = 0,02 * T + 1,7 [kOhm] (V)
Setzt man Gl. V in Gl. IV ein, erhält man:
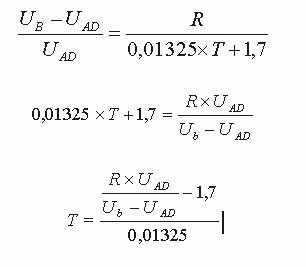 (VI)
(VI)
Die daraus resultierende elektrische Spannung angelegt an den AD-Wandler des Mikrocontrollers ergibt wiederum einen Zahlenwert Z, der sich im Intervall zwischen 0 und 1023 befindet. Der vom AD-Wandler übermittelte Zahlenwert entspricht, wie bereits gezeigt, einer Spannung U zwischen 0 und 5 V. Hier gilt wiederum eine Verhältnisgleichung:
1023 / Z = 5V / U AD (VII)
Diese wird nach U AD aufgelöst und in Gl. VI eingesetzt, so dass man erhält:
U AD = 5V * Z / 1023
und
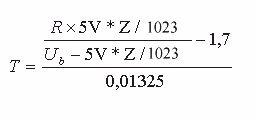 (VIII)
(VIII)
Diese Formel errechnet aus einem Zahlenwert des AD-Wandlers die dazu korrespondierende Temperatur am Sensor. Wie man allerdings erkennen kann, ist der Temperaturbereich, der theroretisch erfasst werden kann, sehr breit. Bei dem hier verwendetenten Sensor KTY 18 ca. 150 K.
Die Auflösung in einem schmalen Temperaturbereich ist demzufolge dagegen gering bzw. grob. Dies ist ungünstig für die Anwendung im Tauchcomputer. Dies gilt insbesondere deshalb, weil für unsere Anwendung nur Temperaturen interessant sind, für die gilt 0°C < T <= 30°C.
Wir werden deshalb auch in diesem Falle wieder einen Messverstärker einsetzen und demzufolge den Sensorspannungsteiler nicht direkt mit dem ADC verbinden. Der Messbreich dieses Verstärkers wird so "gefenstert", dass er den für uns relevanten Temperaturbereich optimal verstärkt. Während beim Drucksensor allerdings ein Messverstärker zum Einsatz kam, der OP-Technik verwandte, reicht für die Temperaturerfassung eine einfache Transistorstufe. Diese hat z. B. folgende Schaltung:
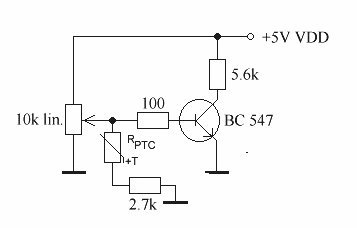
Bild 18: Messverstärker
für Temperatursensor
Auch dieser
Messerverstärker
wird eingemessen. Der Einfachheit halber wird aber hier gleich der
Zahlenwert,
den der AD-Wandler des uC ausgibt, zur Ermittlung der
Funktionsgleichung
herangezogen. Um den Ausgabewert zu erhalten, verändert man die
Software
so, dass an einer Stelle des LCD der vom AD-Wandler erzeugte Zahlenwert
eingeblendet wird. Wird das Programm dann gestartet, so zeigt es dann
den
Ausgabewert des AD-Wandlers direkt auf dem Display an, anhand dessen
mit
einer Wertetabelle die Funktionsgleichung gewonnen werden kann. Diese
wird
dann in eine Programmfunktion integiert, die aus einem
AD-Wandlerergebnis
die Temperatur berechnet. Mit dem 10k
![]() -Regelwiderstand
lässt sich der Messbereich in den optimalen Arbeitspunktbereich
steuern.
Man wird so verfahren, dass bei niedrigster Temperatur (0°C) ein
Zahlenwert
von ca. 500 angezeigt wird. Bei der höchsten Temperatur sollte der
Wert dann um 200 liegen.
-Regelwiderstand
lässt sich der Messbereich in den optimalen Arbeitspunktbereich
steuern.
Man wird so verfahren, dass bei niedrigster Temperatur (0°C) ein
Zahlenwert
von ca. 500 angezeigt wird. Bei der höchsten Temperatur sollte der
Wert dann um 200 liegen.
Doch nun der Reihe nach:
Zuerst die Funtkionen in einem Beispielcode:
In der Funktion main() .
int
main()
{
[...]
for(;;) /* Endlosschleife für Druckmessung und Dekorechnung */
{
/* Sensorabfrage ca. alle 0.25 sec. */
if(loop1b > 500) //500
{
get_dsensor();
get_tsensor(); /* Test für Bestimmung Parameter
Messverstärker
Temperatur */
showtemp(); /* dito */
loop1b = 0;
}
[...]
}
return 0;
}
und in
SIGNAL(SIG_ADC)
{
unsigned char lo, hi;
lo = inp(ADCL);
hi = inp(ADCH);
if(!adc_mode)
depth = hi * 256 + lo;
else
//
temp = ((hi * 256 + lo) - 594) / -7.8;
lcd_putnumber(1,10,hi
* 256 + lo, -1,-1); /* Test für Bestimmung Parameter
Messverstärker
*/
}
Anschließend
taucht man den Sensor in ein Wasserbad in dem unter Zugabe von
Eiswürfeln
und später Warmwasser im Intervall von 0..40°C jeweils in
5K-Schritten
die entsprechenden Temperaturen erzeugt werden. Man erhält dann
eine
Wertetabelle wie diese:
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Den Steigungsfaktor m erhält man wiederum, indem man jeweils für ein Wertepaar berechnet: dy/dx = (y 1 -y 0 )/(x 1 -x 0 ), hier also jeweils einen Zahlenwert des AD-Wandlers minus seinen Nachfolger und das Ganze durch die dazu gehörende Temperaturdifferenz dividieren. Der Y-Achsenabschnitt b ist der Zahlenwert des AD-Wandlers dort wo die Temperatur gleich 0 ist. Somit kann man wiederum eine linerare Funktionsgleichung erhalten, deren Formel in diesem Falle lautet:
Z ADC = -7,8 * T + 594.
T = (Z ADC - 594) / -7.8
Somit ist aus jedem Zahlenergebnis des ADC die als Eingangsgröße vorhandene Temperatur zu ermitteln.
Auf der Basis dieser Daten kann man nun entscheiden, ob eine Temperaturkorrektur der Druckwerte grundsätzlich erforderlich ist oder ob der Drucksensor hinreichend genau auch am unteren Ende des erwarteten Temperaturspektrum ist. Entscheidet man sich für eine Temperaturkompensation, so kann man folgendermaßen verfahren:
Es ist durch die vorher durchgeführten Maßnahmen zur Laufzeit während des Tauchens die jeweilige Temperatur bekannt da diese in der Software aus den Messdaten des Temperatursensors errechnet wird. Unterschreitet diese einen bestimmten Wert (z. B. 10°C), wird ein freier Port des Mikrocontrollers auf "0" gesetzt, also gegen Masse gezogen. Dieser schaltet dann einen zusätzlichen Widerstand im Stromkreis der Nullpunkteinstellung des analogen Sensors und justiert ihn dadurch nach. Den genauen Wert dieses Widerstandes wird man experimentell ermitteln müssen. Dieses Herausfinden des passenden Widerstandswertes ist sehr einfach: Man leitet einen leichten Druck (ca. 50 bis 100 mbar) auf den Sensor und liest die Tiefe am Display ab. Dann legt man den Zusatzwiderstand auf Masse und muss ca. 0.4 bis 0.6 Meter zusätzliche Wassertiefe erhalten.
Beim
SBTC habe ich für den Sensor
SenSym 13U0500PA0K
einen Zusatzwiderstand
von 2.2 M
![]() über
den Anschluss 27 (=Port C5) gegen Masse benutzt, was eine
hinreichend
genaue Tiefenmessung auch bei Wassertemperaturen <10 °C ergibt.
Die Einzelheiten lassen sich aus dem
Schaltplan
des SBTC entnehmen:
über
den Anschluss 27 (=Port C5) gegen Masse benutzt, was eine
hinreichend
genaue Tiefenmessung auch bei Wassertemperaturen <10 °C ergibt.
Die Einzelheiten lassen sich aus dem
Schaltplan
des SBTC entnehmen:
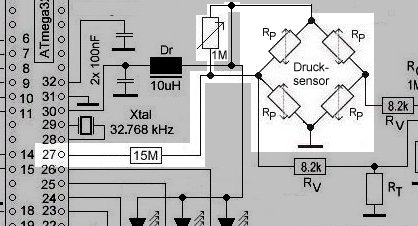
Die Software reagiert folgendermaßen auf einen niedrigen Temperaturwert (innerhalb der Endlosschleife for{;;} in int main() ) :
[...]
/*
Bei kaltem Wasser Sensor nachjustieren */
if(temp <= 10)
cbi(PORTC, 5);
else
sbi(PORTC, 5);
[...]
![]()
Die SBTC-Seiten
Konzeption | LCD-Anzeige | Mikrocontroller | Software | Sensoren | Gehäuse | Erfahrungsberichte